上海复旦大学附中高中三年级（上）期中数学试题 （理科）（分析版）
1、填空题：
1．若集合A={x|x2﹣2x＞0，x∈R}，B={x||x+1|＜0，x∈R}，则A∩B=__________．
2．函数f（x）=log2x+1（x≥4）的反函数f﹣1（x）的概念域是__________．
3．满足等式
=0的复数z为__________．
4．甲校有3600名学生，乙校有5400名学生，丙校有1800名学生．为统计三校学生某方面的状况，计划使用分层抽样法，抽取一个样本容量为90人的样本，则应在甲校抽取的学生数是__________．
5．（x2﹣
）9的二项展开式中，含x3项的系数是__________．
6．直线l1：（a+3）x+y﹣3=0与直线l2：5x+（a﹣3）y+4=0，若l1的方向向量是l2的法向量，则实数a=__________．
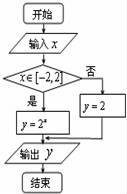
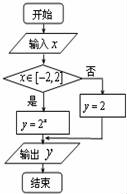
7．阅读程序框图，假如输出的函数值y在区间
内，则输入的实数x的取值范围是__________．
8．已知圆锥的母线长为5cm，侧面积为20πcm2，则此圆锥的体积为__________cm3．
9．在△ABC中，内角A，B，C所对的边分别是a，b，c，已知b﹣c=
a，2sinB=3sinC，则cosplayA的值为__________．
10．数列{an}中，若a1=1，
（n∈N*），则
=__________．
11．甲、乙两人参加法律常识竞赛，共有10道不一样的题目，其中选择题有6道，判断题4道，甲、乙两人依次各抽一题（不可以抽同一题）．则甲、乙中至少有一人抽到选择题的概率等于__________．（用数字作答）
12．已知等差数列{an}满足：
，且它的前n项和Sn有最大值，则当Sn取到最小正值时，n=__________．
13．已知f（x）是概念在R上且周期为3的函数，当x∈[0，3）时，f（x）=|x2﹣2x+
|，若函数y=f（x）﹣a在区间[﹣3，4]上有10个零点（互不相同），则实数a的取值范围是__________．
14．若X是一个非空集合，M是一个以X的某些子集为元素的集合，且满足：
（1）X∈M，Φ∈M；
（2）对于X的任意子集A，B，当A∈M，B∈M时，A∪B∈M，A∩B∈M．则称M是集合X的一个“M﹣集合类”．
比如：M={Φ，{b}，{c}，{b，c}，{a，b，c}}是集合X={a，b，c}的一个“M﹣集合类”．已知集合X={a，b，c}，则所有含{b，c}的“M﹣集合类”的个数为__________．
2、选择题
15．若f（x）和g（x）都是概念在R上的函数，则“f（x）与g（x）同是奇函数或同是偶函数”是“f（x）•g（x）是偶函数”的（）
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
16．已知数列{an}前n项和满足Sn﹣Sn﹣1=
+
（n≥2），a1=1，则an=（）
A．n B．2n﹣1 C．n2 D．2n2﹣1
17．若对任意x∈R，都有f（x）＜f（x+1），那样f（x）在R上 （）
A．肯定单调递增 B．肯定没单调减区间
C．可能没单调增区间 D．肯定没单调增区间
18．设S，T是R的两个非空子集，假如存在一个从S到T的函数y=f（x）满足：（i）T={f（x）|x∈S}；（ii）对任意x1，x2∈S，当x1＜x2时，恒有f（x1）＜f（x2），那样称这两个集合“保序同构”，以下集合对不是“保序同构”的是（）
A．A=N*，B=N
B．A={x|﹣1≤x≤3}，B={x|x=﹣8或0＜x≤10}
C．A={x|0＜x＜1}，B=R
D．A=Z，B=Q
3、解答卷
19．（12分）已知函数f（x）=|x﹣1|，g（x）=﹣x2+6x﹣5．
（1）若g（x）≥f（x），求实数x的取值范围；
（2）求g（x）﹣f（x）的最大值．
20．（14分）已知向量
（m∈R），且
．设y=f（x）．
（1）求f（x）的表达式，并求函数f（x）在
上图象最低点M的坐标．
（2）若对任意
，f（x）＞t﹣9x+1恒成立，求实数t的范围．
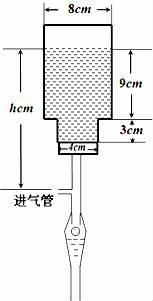
21．（14分）如图所示，一种医用输液瓶可以视为两个圆柱的组合体．开始输液时，滴管内匀速滴下球状液体，其中球状液体的半径
毫米，滴管内液体忽视不计．
（1）假如瓶内的药液恰好156分钟滴完，问每分钟应滴下多少滴？
（2）在条件（1）下，设输液开始后x（单位：分钟），瓶内液面与进气管的距离为h（单位：厘米），已知当x=0时，h=13．试将h表示为x的函数．（注：
1cm3=1000mm3）
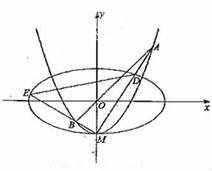
22．（16分）如图，椭圆C1：
+y2=1，x轴被曲线C2：y=x2﹣b截得的线段长等于C1的长半轴长．
（1）求实数b的值；
（2）设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA、MB分别与C1相交于D、E．
①证明：
•
=0；
②记△MAB，△MDE的面积分别是S1，S2．若
=λ，求λ的取值范围．
23．（18分）已知数列{an}满足：a1=1，|an+1﹣an|=pn，n∈N*，Sn为数列{an}的前n项和．
（1）若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；
（2）若p=
，且{a2n﹣1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式；
（3）若p=1，对于给定的正整数n，是不是存在一个满足条件的数列{an}，使得Sn=n，假如存在，给出一个满足条件的数列，假如没有，请说明理由．
2017-2018学年上海复旦大学附中高中三年级（上）期中数学试题 （理科）
参考答案与考试试题分析
1、填空题：
1．（2015秋•杨浦区校级期中）若集合A={x|x2﹣2x＞0，x∈R}，B={x||x+1|＜0，x∈R}，则A∩B=______________________________．
【考试知识点】交集及其运算．
【剖析】分别求出A与B中不等式的解集确定出A与B，找出A与B的交集即可．
【解答】解：由集合A中的不等式变形得：x（x﹣2）＞0，
解得：x＜0或x＞2，
即A=（﹣∞，0）∪（2，+∞）；
由集合B中的不等式，依据绝对值的意义得：x∈∅，
即B=∅，
所以A∩B=∅．
故答案为：∅．
【点评】本题考查了不等式的解法与交集的运算问题，熟练学会交集的概念是解题的重点．
2．（2008•嘉定区校级模拟）函数f（x）=log2x+1（x≥4）的反函数f﹣1（x）的概念域是__________________________________________________．
【考试知识点】反函数．
【剖析】先依据函数单调性求出函数f（x）=log2x+1（x≥4）的值域，然后依据互为反函数图象的关系可知原函数的值域即为反函数的值域．
【解答】解：函数f（x）=log2x+1（x≥4）的值域为[3，+∞），
∴f﹣1（x）的概念域是[3，+∞），
故答案为：[3，+∞）．
【点评】本题主要考查了反函数，与互为反函数图象的关系，是基础题．
3．（2015秋•杨浦区校级期中）满足等式
=0的复数z为__________．
【考试知识点】复数代数形式的乘除运算．
【剖析】借助行列式的性质、复数的运算法则即可得出．
【解答】解：∵等式=0，∴z（1+i）+i（1﹣i）=0，
∴z（1+i）（1﹣i）+i（1﹣i）（1﹣i）=0，
∴2z+2=0，
解得z=﹣1．
故答案为：﹣1．
【点评】本题考查了行列式的性质、复数的运算法则，考查了推理能力与计算能力，是基础题．
4．（2014•浦东新区一模）甲校有3600名学生，乙校有5400名学生，丙校有1800名学生．为统计三校学生某方面的状况，计划使用分层抽样法，抽取一个样本容量为90人的样本，则应在甲校抽取的学生数是__________．
【考试知识点】分层抽样办法．
【剖析】依据分层抽样的概念，即可确定甲校抽取的人数．
【解答】解：∵甲校，乙校，丙校的学生的人数之比为：3600：5400：
1800=2：3：
1，
∴抽取一个样本容量为90人的样本，则应在甲校抽取的学生数为：
，
故答案为：30．
【点评】本题主要考分数查询层抽样的概念和应用，依据分层抽样的概念确定对应的抽取比率是解决本题的重点，比较基础．
5．（2015秋•杨浦区校级期中）（x2﹣
）9的二项展开式中，含x3项的系数是__________．
【考试知识点】二项式系数的性质．
【剖析】在二项展开式的通项公式中，令x的指数等于3，求出r的值，即可求得展开式中含x3项的系数．
【解答】解：（x2﹣）9的二项展开式中，通项公式为
Tr+1=
•（﹣1）r•x18﹣3r，
令18﹣3r=3，求得r=5，
故展开式中含x3项的系数为﹣
=﹣126．
故答案为：﹣126．
【点评】本题主要考查了二项式定理的应用问题，借助展开式的通项公式求二项式系数，是基础题．
6．（2014•徐汇区一模）直线l1：（a+3）x+y﹣3=0与直线l2：5x+（a﹣3）y+4=0，若l1的方向向量是l2的法向量，则实数a=__________．
【考试知识点】两条直线垂直与倾斜角、斜率的关系．
【剖析】先分别求出两直线的方向向量，然后依据l1的方向向量是l2的法向量，则两直线的方向向量垂直，最后依据互相垂直的向量的数目积为0，从而求出所求．
【解答】解：∵直线l1：（a+3）x+y﹣3=0与直线l2：5x+（a﹣3）y+4=0，
∴直线l1的方向向量为=（1，﹣（a+3）），
直线l2的方向向量为=（1，
），
∵l1的方向向量是l2的法向量，
∴两直线的方向向量垂直，即•=1×1+（﹣a﹣3）×=0，解得a=﹣2，
∴实数a=﹣2．
故答案为：﹣2．
【点评】本题主要考查了直线的方向向量与法向量，与借助空间向量数目积的运算，同时考查了运算求解的能力，是基础题．
7．（2014•松江区三模）阅读程序框图，假如输出的函数值y在区间内，则输入的实数x的取值范围是__________________________________________________．
【考试知识点】程序框图．
【剖析】由程序框图得出分段函数，依据函数的值域，求出实数x的取值范围．
【解答】解：由程序框图可得分段函数：y=
，
∴令2x∈[
，1]，则x∈[﹣2，0]，满足题意；
∴输入的实数x的取值范围是[﹣2，0]．
故答案为：[﹣2，0]．
【点评】本题考查了程序框图的运行过程的问题，解题时应了解框图，得出分段函数，从而做出正确解答，是基础题．
8．（2014•嘉定区一模）已知圆锥的母线长为5cm，侧面积为20πcm2，则此圆锥的体积为__________cm3．
【考试知识点】旋转体（圆柱、圆锥、圆台）．
【剖析】依据圆锥的侧面积和圆锥的母线长，代入圆锥的侧面积公式求得圆锥的底面半径，再求得圆锥的高，代入体积公式计算．
【解答】解：∵圆锥的母线长是5cm，侧面积是20πcm2，
设圆锥的半径为r，
∴有πr×5=20π⇒r=4，
∴圆锥的高为
=3，
∴圆锥的体积为
×π×r2×3=16πcm3．
故答案：
16πcm3．
【点评】本题考查了圆锥的侧面积公式、体积公式，解题的重点是求得圆锥的半径．
9．（2014•天津）在△ABC中，内角A，B，C所对的边分别是a，b，c，已知b﹣c=a，2sinB=3sinC，则cosplayA的值为____________________．
【考试知识点】余弦定理；正弦定理．
【剖析】由条件借助正弦定理求得a=2c，b=，再由余弦定理求得cosplayA=
的值．
【解答】解：在△ABC中，
∵b﹣c=
a ①，2sinB=3sinC，
∴2b=3c ②，
∴由①②可得a=2c，b=
．
再由余弦定理可得 cosplayA===﹣，
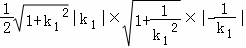故答案为：﹣．
【点评】本题主要考查正弦定理、余弦定理的应用，是中档题．
10．（2014•普陀区一模）数列{an}中，若a1=1，
（n∈N*），则
=____________________．
【考试知识点】数列的求和．
【剖析】由，求出a1+a2+a3+a4+…+a2n﹣1+a2n，然后求得极限．
【解答】解：由
，得（a1+a2）+（a3+a4）+…+（a2n﹣1+a2n）=
=
=，
∴
=
=
，
故答案为：．
【点评】本题考查数列求和、数列极限，属基础题，准确求出数列的和是解题重点．
11．（2015秋•杨浦区校级期中）甲、乙两人参加法律常识竞赛，共有10道不一样的题目，其中选择题有6道，判断题4道，甲、乙两人依次各抽一题（不可以抽同一题）．则甲、乙中至少有一人抽到选择题的概率等于____________________．（用数字作答）
【考试知识点】古典概型及其概率计算公式．
【剖析】先求出基本事件总数和甲、乙都抽到判断题包括的基本事件个数，由此借助对立事件概率计算公式能求出甲、乙中至少有一人抽到选择题的概率．
【解答】解：甲、乙两人参加法律常识竞赛，共有10道不一样的题目，其中选择题有6道，判断题4道，
甲、乙两人依次各抽一题（不可以抽同一题）．
基本事件总数n=10×9=90，
甲、乙都抽到判断题包括的基本事件个数m=4×3=12，
∴甲、乙中至少有一人抽到选择题的概率：
p=1﹣
=1﹣
=．
故答案为：．
【点评】本题考查概率的求法，是基础题，解题时要认真审题，注意对立事件概率计算公式的合理运用．
12．（2016秋•承德期中）已知等差数列{an}满足：
，且它的前n项和Sn有最大值，则当Sn取到最小正值时，n=__________．
【考试知识点】等差数列的性质；数列的函数特质．
【剖析】依据题意看出d＜0、a10＞0＞a11、a10+a11＜0，借助前n项和公式和性质看出S20＜0、S19＞0，再借助数列的单调性看出当Sn取的最小正值时n的值．
【解答】解：由题意知，Sn有最大值，所以d＜0，
由，所以a10＞0＞a11，
且a10+a11＜0，
所以S20=10（a1+a20）=10（a10+a11）＜0，
则S19=19a10＞0，
又a1＞a2＞…＞a10＞0＞a11＞a12
所以S10＞S9＞…＞S2＞S1＞0，S10＞S11＞…＞S19＞0＞S20＞S21
又S19﹣S1=a2+a3+…+a19=9（a10+a11）＜0，
所以S19为最小正值．
故答案为：
10．
【点评】本题考查了等差数列的性质、前n项和公式与Sn最值问题，需要Sn获得最小正值时n的值，重点是要找出什么时间an+1小于0且an大于0．
13．（2014•江苏）已知f（x）是概念在R上且周期为3的函数，当x∈[0，3）时，f（x）=|x2﹣2x+|，若函数y=f（x）﹣a在区间[﹣3，4]上有10个零点（互不相同），则实数a的取值范围是____________________．
【考试知识点】根的存在性及根的个数判断．
【剖析】在同一坐标系中画出函数的图象与直线y=a的图象，借助数形结合判断a的范围即可．
【解答】解：f（x）是概念在R上且周期为3的函数，当x∈[0，3）时，f（x）=|x2﹣2x+|，若函数y=f（x）﹣a在区间[﹣3，4]上有10个零点（互不相同），在同一坐标系中画出函数f（x）与y=a的图象如图：由图象可知．
故答案为：（0，）．
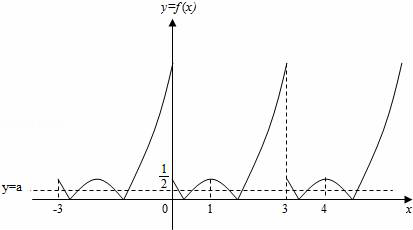
【点评】本题考查函数的图象以函数的零点的求法，数形结合的应用．
14．（2015秋•杨浦区校级期中）若X是一个非空集合，M是一个以X的某些子集为元素的集合，且满足：
（1）X∈M，Φ∈M；
（2）对于X的任意子集A，B，当A∈M，B∈M时，A∪B∈M，A∩B∈M．则称M是集合X的一个“M﹣集合类”．
比如：M={Φ，{b}，{c}，{b，c}，{a，b，c}}是集合X={a，b，c}的一个“M﹣集合类”．已知集合X={a，b，c}，则所有含{b，c}的“M﹣集合类”的个数为__________．
【考试知识点】并集及其运算．
【剖析】依据新概念以集合为元素组成集合，由题意知M﹣集合类集合至少含有三个元素：∅，{b，c}，{a，b，c}，然后再研究其它几个元素的添加方法有多少个，可分添加元素的个数分为0，1，2，3，4，5共六类进行讨论得出结论．
【解答】解：依题意知，M中至少含有这几个元素：∅，{b，c}，{a，b，c}，将它看成一个整体；
剩余的{a}、{b}、{c}、{a，c}、{a，b}共5个，{a，b}和{b}需要同时在M中，{a，c}和{c}需要同时在M中；
①{a}、{b}、{c}、{a，c}、{a，b}添加0个的集合为{∅，{b，c}，{a，b，c}}，一种
②{a}、{b}、{c}、{a，c}、{a，b}添加1个的集合为{∅，{a}，{b，c}，{a，b，c}}，{∅、{b}，{b，c}，{a，b，c}}，{∅、{c}，{b，c}，{a，b，c}}，共三种
③{a}、{b}、{c}、{a，c}、{a，b}添加2个的集合共3种即{b}、{c}；{c}、{a，c}；{b}、{a，b}三种添加方法
④{a}、{b}、{c}、{a，c}、{a，b}添加3个的集合共2种，即：{b}、{c}、{a，c}；④{a}、{b}、{a，b}二种
⑤{a}、{b}、{c}、{a，c}、{a，b}添加4个的集合共0种
⑥{a}、{b}、{c}、{a，c}、{a，b}添加5个的集合共1种
综上讨论知，共10种
故答案为：
10．
【点评】本题是一道新概念，比较麻烦，注意M﹣集合类满足的条件，依据M﹣集合类的元素个数进行书写，会便捷些，是中档题．
2、选择题
15．（2015秋•杨浦区校级期中）若f（x）和g（x）都是概念在R上的函数，则“f（x）与g（x）同是奇函数或同是偶函数”是“f（x）•g（x）是偶函数”的（）
A．充分非必要条件 B．必要非充分条件
C．充要条件 D．既非充分又非必要条件
【考试知识点】必要条件、充分条件与充要条件的判断．
【剖析】借助偶函数的断定办法、浅易逻辑的断定办法即可得出．
【解答】解：由“f（x）与g（x）同是奇函数”可得“f（x）•g（x）是偶函数”；
反之不成立，比如可能f（x）与g（x）同是偶函数．
因此“f（x）与g（x）同是奇函数”是“f（x）•g（x）是偶函数”的充分非必要条件．
故选：A．
【点评】本题考查了偶函数的断定办法、浅易逻辑的断定办法，考查了推理能力与计算能力，是基础题．
16．（2015秋•杨浦区校级期中）已知数列{an}前n项和满足Sn﹣Sn﹣1=
+ （n≥2），a1=1，则an=（）
A．n B．2n﹣1 C．n2 D．2n2﹣1
【考试知识点】数列递推式．
【剖析】借助平方差公式对已知数列递推式化简整理，求得
=1，依据等差数列的概念看出数列{}是一个首项为1公差为1的等差数列．求得数列{
}的通项公式，再由an=Sn﹣Sn﹣1求得an ．
【解答】解：由Sn﹣Sn﹣1=+
，得
=+，
∴
，
∴数列{}是一个首项为1公差为1的等差数列．
∴=1+（n﹣1）×1=n，
∴Sn=n2．
当n≥2，an=Sn﹣Sn﹣1=n2﹣（n﹣1）2=2n﹣1；
a1=1合适上式，
∴an=2n﹣1，
故选：B．
【点评】本题考查数列递推式，考查了等差关系的确定，练习了由数列的前n项和求数列的通项公式，是中档题．
17．（2015秋•杨浦区校级期中）若对任意x∈R，都有f（x）＜f（x+1），那样f（x）在R上 （）
A．肯定单调递增 B．肯定没单调减区间
C．可能没单调增区间 D．肯定没单调增区间
【考试知识点】函数单调性的性质．
【剖析】依据对任意x∈R，都有f（x）＜f（x+1），依据函数的单调性的概念可得结论．
【解答】解：若f（x）是增函数，则由x＜x+1可知f（x）＜f（x+1）肯定成立，但F（x）＜F（x+1）
并不可以保证f（x）＜f（x+0.5），譬如令f（x）=x+sin2πx
则f（x+1）=x+1+sin2πx=f（x）+1＞f（x）但显然它不单调，因此，没办法证明f（x）是增函数，
同理，函数f（x）可能没单调增区间，可能没单调减区间．
故选C．
【点评】本题考查了对函数单调性的概念的理解和运用能力．比较基础．
18．（2013•福建）设S，T是R的两个非空子集，假如存在一个从S到T的函数y=f（x）满足：（i）T={f（x）|x∈S}；（ii）对任意x1，x2∈S，当x1＜x2时，恒有f（x1）＜f（x2），那样称这两个集合“保序同构”，以下集合对不是“保序同构”的是（）
A．A=N*，B=N
B．A={x|﹣1≤x≤3}，B={x|x=﹣8或0＜x≤10}
C．A={x|0＜x＜1}，B=R
D．A=Z，B=Q
【考试知识点】函数单调性的判断与证明．
【剖析】借助题目给出的“保序同构”的定义，对每个选项中给出的两个集合，借助所学常识，找出可以使两个集合满足题目所给出的条件的函数，即B是函数的值域，且函数为概念域上的增函数．排除掉是“保序同构”的，即可得到要选择的答案．
【解答】解：对于A=N*，B=N，存在函数f（x）=x﹣1，x∈N*，满足：（i）B={f（x）|x∈A}；（ii）对任意x1，x2∈A，当x1＜x2时，恒有f（x1）＜f（x2），所以选项A是“保序同构”；
对于A={x|﹣1≤x≤3}，B={x|x=﹣8或0＜x≤10}，存在函数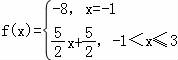，满足：
（i）B={f（x）|x∈A}；（ii）对任意x1，x2∈A，当x1＜x2时，恒有f（x1）＜f（x2），所以选项B是“保序同构”；
对于A={x|0＜x＜1}，B=R，存在函数f（x）=tan（），满足：（i）B={f（x）|x∈A}；
（ii）对任意
x1，x2∈A，当x1＜x2时，恒有f（x1）＜f（x2），所以选项C是“保序同构”；
前三个选项中的集合对是“保序同构”，由排除法可知，不是“保序同构”的只有D．
故选D．
【点评】本题是新概念题，考查了函数的概念域和值域，考查了函数的单调性，综合考查了不相同种类型函数的基本性质，是基础题．
3、解答卷
19．（12分）（2014•徐汇区一模）已知函数f（x）=|x﹣1|，g（x）=﹣x2+6x﹣5．
（1）若g（x）≥f（x），求实数x的取值范围；
（2）求g（x）﹣f（x）的最大值．
【考试知识点】函数的最值及其几何意义．
【剖析】（1）去掉f（x）的绝对值，由g（x）≥f（x），求出x的取值范围；
（2）由（1）知g（x）﹣f（x）的最大值在[1，4]上获得，求出即可．
【解答】解：（1）当x≥1时，f（x）=x﹣1；
∵g（x）≥f（x），
∴﹣x2+6x﹣5≥x﹣1；
整理，得（x﹣1）（x﹣4）≤0，
解得x∈[1，4]；
当x＜1时，f（x）=1﹣x；
∵g（x）≥f（x），
∴﹣x2+6x﹣5≥1﹣x，
整理，得（x﹣1）（x﹣6）≤0，
解得x∈[1，6]，又，
∴x∈∅；
综上，x的取值范围是[1，4]．
（2）由（1）知，g（x）﹣f（x）的最大值在[1，4]上获得，
∴g（x）﹣f（x）=（﹣x2+6x+5）﹣（x﹣1）=﹣+≤，
∴当x=
时，g（x）﹣f（x）取到最大值是．
【点评】本题考查了含有绝对值的函数的应用问题，解题时应先去掉绝对值，再进行讨论解答．
20．（14分）（2010•浦东新区二模）已知向量（m∈R），且
．设y=f（x）．
（1）求f（x）的表达式，并求函数f（x）在
上图象最低点M的坐标．
（2）若对任意，f（x）＞t﹣9x+1恒成立，求实数t的范围．
【考试知识点】向量的加法及其几何意义；函数恒成立问题；三角函数的最值．
【剖析】（1）依据所给的向量之间的关系，写出关于三角函数的关系式，消元得到函数式，整理成可以解决三角函数性质的形式，依据所给的变量的范围得到三角函数的范围．
（2）本题是一个函数的恒成立问题，写出关系式，离别参数，要证一个变量恒小于一个函数式时，要用一种函数思想，即只须这个变量小于函数的最小值即可．
【解答】解：（1）∵
，即，
消去m，得，
即，
时，
，，
即f（x）的最小值为1，此时
∴函数f（x）的图象上最低点M的坐标是
（2）∵f（x）＞t﹣9x+1，即，
当
时，函数单调递增，y=9x单调递增，
∴
在
上单调递增，
∴
的最小值为1，
为要恒成立，只须t+1＜1，
∴t＜0为所求．
【点评】本题是一个三角函数同向量结合的问题，是以向量平行的充要条件为条件，得到三角函数的关系式，是一道综合题，在高考考试时可以以选择和填空形式出现．
21．（14分）（2014•普陀区一模）如图所示，一种医用输液瓶可以视为两个圆柱的组合体．开始输液时，滴管内匀速滴下球状液体，其中球状液体的半径
毫米，滴管内液体忽视不计．
（1）假如瓶内的药液恰好156分钟滴完，问每分钟应滴下多少滴？
（2）在条件（1）下，设输液开始后x（单位：分钟），瓶内液面与进气管的距离为h（单位：厘米），已知当x=0时，h=13．试将h表示为x的函数．（注：
1cm3=1000mm3）
【考试知识点】函数模型的选择与应用．
【剖析】（1）设每分钟滴下k（k∈N*）滴，由圆柱的体积公式求出瓶内液体的体积，再求出k滴球状液体的体积，得到156分钟所滴液体体积，由体积相等得到k的值．
（2）由（1）知，每分钟滴下πcm3药液，当液面高度离进气管4至13cm时，x分钟滴下液体的体积等于大圆柱的底面积乘以（13﹣h），当液面高度离进气管1至4cm时，x分钟滴下液体的体积等于大圆柱的体积与小圆柱底面积乘以（4﹣h）的和，由此即可得到瓶内液面与进气管的距离为h与输液时间x的函数关系．
【解答】解：（1）设每分钟滴下k（k∈N*）滴，
则瓶内液体的体积cm3，
k滴球状液体的体积cm3，
∴，解得k=75，故每分钟应滴下75滴．
（2）由（1）知，每分钟滴下πcm3药液，
当4≤h≤13时，xπ=π•42•（13﹣h），即，此时0≤x≤144；
当1≤h＜4时，xπ=π•42•9+π•22•（4﹣h），即
，此时144＜x≤156．
综上可得
．
【点评】本题考查了函数模型的选择及应用，考查了简单的数学建模思想办法，解答的重点是对题意的理解，然后正确列出体积相等的关系式，属中档题．
22．（16分）（2012•日照二模）如图，椭圆C1： +y2=1，x轴被曲线C2：y=x2﹣b截得的线段长等于C1的长半轴长．
（1）求实数b的值；
（2）设C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA、MB分别与C1相交于D、E．
①证明： •=0；
②记△MAB，△MDE的面积分别是S1，S2．若=λ，求λ的取值范围．
【考试知识点】圆锥曲线的综合．
【剖析】（1）确定半长轴为2，借助x轴被曲线C2：y=x2﹣b截得的线段长等于C1的长半轴长，可求b的值；
（2）①设直线的方程与抛物线方程联立，借助点M的坐标为（0，﹣1），可得kMAkMB=﹣1，从而得证；
②设直线的斜率为k1，则直线的方程为y=k1x﹣1，代入抛物线方程可得x2=k1x，从而可得点A的坐标、点B的坐标，进而可得S1，同理可得S2，进而可得比值，由此可得λ的取值范围．
【解答】（1）解：由题意知：半长轴为2，则有2
=2 …（3分）
∴b=1 …（4分）
（2）①证明：由题意知，直线l的斜率存在，设为k，则直线的方程为y=kx．
与抛物线方程联立，消去y可得x2﹣kx﹣1=0，…（6分）
设A（x1，y1），B（x2，y2），则x1，x2是上述方程的两个实根，于是x1+x2=k，x1x2=﹣1．…（7分）
又点M的坐标为（0，﹣1），所以kMAkMB=×=
=﹣1…（9分）
故MA⊥MB，即MD⊥ME，故
…（10分）
②设直线的斜率为k1，则直线的方程为y=k1x﹣1，代入抛物线方程可得x2=k1x，解得x=0或x=k1，则点A的坐标为（k1，） …（12分）
同理可得点B的坐标为．
于是==
直线的方程为y=k1x﹣1，代入椭圆方程，消去y，可得（）x2﹣8k1x=0，解得x=0或x=，则点D的坐标为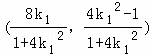； …（14分）
同理可得点E的坐标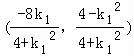
于是S2==
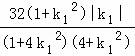
因此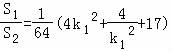，…（16分）
又由点A，B的坐标可知，k==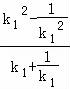
，平方后代入上式，
所以λ=
故λ的取值范围为[）． …（18分）
【点评】本题考查椭圆的规范方程，考查直线与抛物线、椭圆的地方关系，考查三角形面积的计算，是中档题．
23．（18分）（2015秋•杨浦区校级期中）已知数列{an}满足：a1=1，|an+1﹣an|=pn，n∈N*，Sn为数列{an}的前n项和．
（1）若{an}是递增数列，且a1，2a2，3a3成等差数列，求p的值；
（2）若p=，且{a2n﹣1}是递增数列，{a2n}是递减数列，求数列{an}的通项公式；
（3）若p=1，对于给定的正整数n，是不是存在一个满足条件的数列{an}，使得Sn=n，假如存在，给出一个满足条件的数列，假如没有，请说明理由．
【考试知识点】数列的求和；数列的应用．
【剖析】（1）借助）{an}是递增数列，且a1，2a2，3a3成等差数列，得到关于p的方程解之；
（2）将p代入，借助累加法得到数列{an}的通项公式；
（3）由p=1得到|an+1﹣an|=1，而a1=1，得到后面的各项，察看剖析规律，找到满足满足Sn=n的各项．
【解答】解：（1）{an}是递增数列，且a1，2a2，3a3成等差数列，4a2=a1+3a3，又a2﹣a1=p，a3﹣a2=p2，所以3p2﹣p=0，解得p=或者p=0（舍去）
（2）p=，且{a2n﹣1}是递增数列，{a2n}是递减数列，所以a2n﹣a2n﹣1＞0，a2n+1﹣a2n＜0，
，，
所以an=a1+（a2﹣a1）+（a3﹣a2）+…（an﹣an﹣1）=1﹣+…+
=；
（3）由题意得|an+1﹣an|=1，而a1=1，
所以a2=2，0；a3=3，1，﹣1；a4=4，2，0，﹣2…
所以S1=1，S2=3，1；S3=6，4，2，0；S4=10，8，6，4，0，﹣2…
即S4k﹣3为奇数；S4k﹣2为偶数；S4k为偶数；因此只有S4k﹣3，S4k满足Sn=n．
【点评】本题考查了数列求和与数列递推关系的运用；是难点．
